Wirtschaftliche Verflechtungen
Bei wirtschaftlichen Verflechtungen ist es oft hilfreich diese als Matrix darzustellen, um bestimmte Beziehungen erkennen zu können, z.B. wie viele Zwischenprodukte du für ein Endprodukt benötigst.
Bevor du eine Matrix erstellst, solltest du zunächst in einer Tabelle die entsprechenden Werte mit ihrer Beziehung eintragen:
Die Werte der Tabelle geben dir an, wie viele Einheiten B für je eine Einheit A benötigt werden.
Diese Tabelle kannst du nun in eine Matrix übertragen.
Nun kannst du aus der Matrix z.B. herauslesen, wie viel du für eine ME von A1 benötigst: 3 ME von B1, 1 ME von B2 und von B3.
| A1 | A2 | A3 | |
|---|---|---|---|
| B1 | 3 | 4 | 5 |
| B2 | 1 | 2 | 3 |
| B3 | 4 | 3 | 2 |
1.
Eine Süßigkeitenfabrik stellt 4 verschiedene Endprodukte her:
 ), Kakao (
), Kakao ( ) und Gelatine (
) und Gelatine ( ) man für die Herstellung von jeweils 1 ME Endprodukt enthalten ist:
) man für die Herstellung von jeweils 1 ME Endprodukt enthalten ist:
- Schokoladentafeln (
)
- Gummibärchen (
)
- Saure Zungen (
)
- Kekse (
)

a)
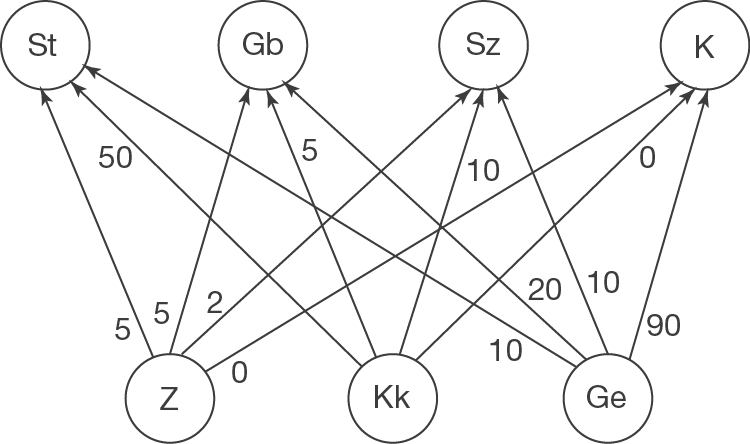
Beschreibe die Verteilung der Zwischenprodukte auf die Endprodukte in Form einer Zwischenprodukt-Endprodukt-Matrix.
b)
Die Elemente der in Teil a bestimmten Zwischenprodukt-Endprodukt-Matrix  geben jeweils an, wie viele ME der Zwischenprodukte
geben jeweils an, wie viele ME der Zwischenprodukte  ,
,  und
und  jeweils für die Herstellung von 1 ME der Endprodukte
jeweils für die Herstellung von 1 ME der Endprodukte  ,
,  ,
,  und
und  benötigt werden.
Wie lässt sich diese Matrix
benötigt werden.
Wie lässt sich diese Matrix  auf je 10 ME Endprodukte umrechnen?
auf je 10 ME Endprodukte umrechnen?
c)
Die folgende Matrix
 gibt die auf 1 ME bezogene Zusammensetzung der neuen Produktlinie für die Endprodukte
gibt die auf 1 ME bezogene Zusammensetzung der neuen Produktlinie für die Endprodukte  ,
,  ,
,  und
und  an.
Stelle die Zu- bzw. Abnahme der Anteile der einzelnen Zwischenprodukte im Vergleich zur Matrix
an.
Stelle die Zu- bzw. Abnahme der Anteile der einzelnen Zwischenprodukte im Vergleich zur Matrix  in einer neuen Matrix an.
in einer neuen Matrix an.
d)
Wollen die Kunden Süßigkeiten bestellen, so geben sie ihre Bestellmengen in ME für die Endprodukte in Form von Listen bzw. Spaltenvektoren an. Eine Bestellung von 7 ME Schokoladentafeln ( ), 3 ME Gummibärchen (
), 3 ME Gummibärchen ( ), 4 ME Saure Zungen (
), 4 ME Saure Zungen ( ) und 11 ME Kekse (
) und 11 ME Kekse ( ) schreibt sich also als folgender Produktionsvektor:
) schreibt sich also als folgender Produktionsvektor:
 Wie viele ME der Zwischenprodukte
Wie viele ME der Zwischenprodukte  ,
,  und
und  werden für die Realisierung dieses Auftrages benötigt? Gib dein Ergebnis in Form eines Zwischenproduktvektors
werden für die Realisierung dieses Auftrages benötigt? Gib dein Ergebnis in Form eines Zwischenproduktvektors  an.
an.
2.
Ein Schmelzofen, der die Legierungen (Endprodukte) Super-Hart  und Ultra-Hart
und Ultra-Hart  herstellt, verwendet zur Produktion die Rohstoffe Titan
herstellt, verwendet zur Produktion die Rohstoffe Titan  , Eisen
, Eisen  und Wolfram
und Wolfram  . Die folgende Input-Output-Tabelle bzw. die Rohstoff-Endprodukt-Matrix gibt dir dazu an, wie viele kg Rohstoffe für die Produktion von 1 kg Endprodukt benötigt werden.
. Die folgende Input-Output-Tabelle bzw. die Rohstoff-Endprodukt-Matrix gibt dir dazu an, wie viele kg Rohstoffe für die Produktion von 1 kg Endprodukt benötigt werden.
| Endprodukte | |||
| 1 | 3 | ||
| Rohstoffe | 1 | 4 | |
| 2 | 3 | ||
a)
Bestimme, ausgehend von der oben gegebenen Input-Output-Tabelle bzw. die Rohstoff-Endprodukt-Matrix, das zugehörige Verflechtungsdiagramm.
b)
Formuliere die Matrizengleichung, die den allgemeinen Zusammenhang zwischen dem Produktionsvektor  und dem zugehörigen Rohstoffvektor
und dem zugehörigen Rohstoffvektor  beschreibt.
beschreibt.
c)
Berechne, wie viele Rohstoffe  ,
,  und
und  benötigt werden, um 6 kg
benötigt werden, um 6 kg  - und 3 kg
- und 3 kg  -Legierung herzustellen. Formuliere dein Ergebnis als Rohstoffvektor
-Legierung herzustellen. Formuliere dein Ergebnis als Rohstoffvektor  .
.
d)
Im Lager des Schmelzofens liegen 70 kg Titan, 90 kg Eisen und 80 kg Wolfram bereit. Berechne nun, wie viele kg Super-Hart und Ultra-Hart Legierung damit hergestellt werden können. Gib dein Ergebnis als Endproduktvektor  an.
an.
3.
Ein Betrieb der pharmazeutischen Industrie stellt zwei Präparate her, das Präparat Super-Fit  und das Präparat Guter-Schlaf
und das Präparat Guter-Schlaf  . Zur Herstellung dieser Präparate werden als Rohstoffe drei Vitamine, Vitamin A (
. Zur Herstellung dieser Präparate werden als Rohstoffe drei Vitamine, Vitamin A ( ), Vitamin B (
), Vitamin B ( ) und Vitamin C (
) und Vitamin C ( ) verwendet. Weiterhin fallen bei der Produktion die Zwischenprodukte
) verwendet. Weiterhin fallen bei der Produktion die Zwischenprodukte  ,
,  und
und  an.
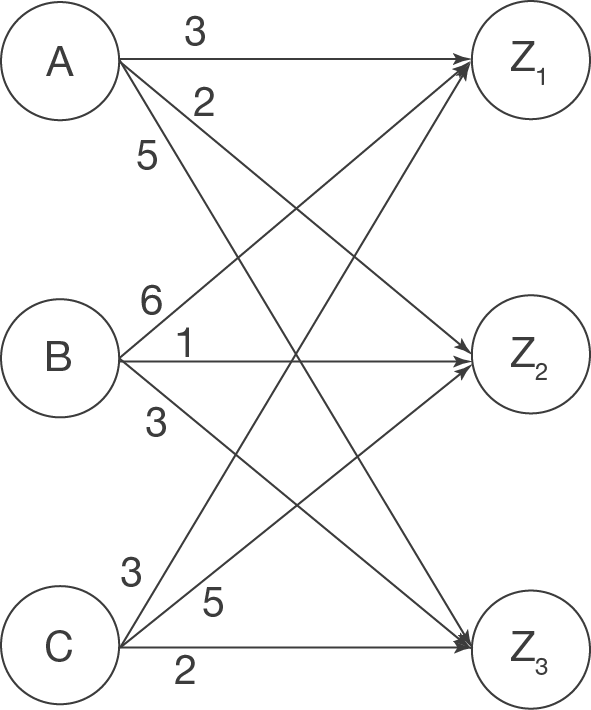
Der Verflechtungsgraph auf der linken Seite gibt dir dazu an, wie viel Mengeneinheiten (ME) Rohstoffe
an.
Der Verflechtungsgraph auf der linken Seite gibt dir dazu an, wie viel Mengeneinheiten (ME) Rohstoffe  ,
,  und
und  für die Produktion einer ME der Zwischenprodukte
für die Produktion einer ME der Zwischenprodukte  und
und  verwendet werden müssen, während die Zwischenprodukt-Endprodukt-Matrix auf der rechten Seite dir angibt, wie viele ME der Zwischenprodukte verwendet werden müssen, um jeweils eine ME der Endprodukte
verwendet werden müssen, während die Zwischenprodukt-Endprodukt-Matrix auf der rechten Seite dir angibt, wie viele ME der Zwischenprodukte verwendet werden müssen, um jeweils eine ME der Endprodukte  und
und  herzustellen.
herzustellen.

| Endprodukte | ||
| Zwischenprodukte | ||
| 2 | 4 | |
| 3 | 7 | |
| 5 | 1 | |
a)
Bestimme ausgehend vom Verflechtungsgraphen die Rohstoff-Zwischenprodukt-Matrix und gib den vollständigen zweistufigen Verflechtungsgraph an.
b)
Formuliere die Matrizengleichung, die den allgemeinen Zusammenhang zwischen dem Produktionsvektor  und dem zugehörigen Rohstoffvektor
und dem zugehörigen Rohstoffvektor  beschreibt und bestimme dazu die Rohstoff-Endprodukt-Matrix.
beschreibt und bestimme dazu die Rohstoff-Endprodukt-Matrix.
c)
Ein Großkunde bestellt 100 ME der Super-Fit und 200 ME der Guter-Schlaf Präparate. Wie viele ME an Rohstoffen  ,
,  und
und  werden dazu benötigt?
Wie viele ME der Zwischenprodukte
werden dazu benötigt?
Wie viele ME der Zwischenprodukte  ,
,  und
und  werden für diesen Auftrag benötigt?
werden für diesen Auftrag benötigt?
d)
Ein anderer Kunde bestellt 100 ME von  und 150 ME von
und 150 ME von  . Aus dem Zwischenlager werden dazu 200 ME von
. Aus dem Zwischenlager werden dazu 200 ME von  und 100 ME von
und 100 ME von  für die Produktion verwendet.
Wie viele ME der einzelnen Rohstoffe werden für diesen Auftrag dann noch benötigt?
für die Produktion verwendet.
Wie viele ME der einzelnen Rohstoffe werden für diesen Auftrag dann noch benötigt?
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Verteilung durch eine Zwischenprodukt-Endprodukt-Matrix beschreiben
Beschreibe den gegebenen Verflechtungsgraphen, der die Verteilung der Zwischenprodukte auf die Endprodukte angibt, durch eine Zwischenprodukt-Endprodukt-Matrix. Diese setzt sich so zusammen:
 entspricht also einer
entspricht also einer  -Matrix. Beim Erstellen dieser Matrix
-Matrix. Beim Erstellen dieser Matrix  kann es hilfreich sein, wenn du diese und deren Einträge zunächst in einer Tabelle einträgst:
kann es hilfreich sein, wenn du diese und deren Einträge zunächst in einer Tabelle einträgst:
Aus dieser Tabelle ergibt sich die hier gesuchte Matrix  :
:

- Sie besitzt genau so viele Zeilen, wie es Zwischenprodukte gibt
Die Matrix hat insgesamt 3 Zeilen
- Sie besitzt genau so viele Spalten, wie es Endprodukte gibt.
Die Matrix hat insgesamt 4 Spalten
- Die Matrixeinträge ergeben sich aus den Mengeneinheiten der Zwischenprodukte, die für eine ME eines Endproduktes nötig sind
| Endprodukte | ||||
| Zwischenprodukte | ||||
| 5 | 5 | 2 | 0 | |
| 50 | 5 | 10 | 0 | |
| 10 | 20 | 10 | 90 | |
b)
Umrechnen der Matrix  auf je 10 ME Endprodukte
Die von dir erstellte Matrix
auf je 10 ME Endprodukte
Die von dir erstellte Matrix  gibt an, wie viele ME Zwischenprodukte man für 1 ME eines jeweiligen Endproduktes benötigt. Deine Aufgabe ist es nun, die Matrix
gibt an, wie viele ME Zwischenprodukte man für 1 ME eines jeweiligen Endproduktes benötigt. Deine Aufgabe ist es nun, die Matrix  so zu modifizieren, dass diese angibt, wie viele ME Zwischenprodukte man für jeweils 10 ME eines jeweiligen Endproduktes benötigt.
Willst du diese veränderte Matrix
so zu modifizieren, dass diese angibt, wie viele ME Zwischenprodukte man für jeweils 10 ME eines jeweiligen Endproduktes benötigt.
Willst du diese veränderte Matrix  bestimmen, so multiplizierst du die ursprüngliche Matrix
bestimmen, so multiplizierst du die ursprüngliche Matrix  mit 10. Multipliziere dazu jeden einzelnen Matrixeintrag mit 10.
Die hier gesuchte Matrix
mit 10. Multipliziere dazu jeden einzelnen Matrixeintrag mit 10.
Die hier gesuchte Matrix  ergibt sich also zu:
Die hier gesuchte Matrix ist also:
ergibt sich also zu:
Die hier gesuchte Matrix ist also:

c)
Darstellen der Zu- und Abnahmen in einer neuen Matrix
Die in der Aufgabenstellung gegebene Matrix  gibt die auf 1 ME bezogene Zusammensetzung einer neuen Produktlinie für die Endprodukte
gibt die auf 1 ME bezogene Zusammensetzung einer neuen Produktlinie für die Endprodukte  ,
,  ,
,  und
und  an. Deine Aufgabe ist es nun, die Zu- und Abnahme der Anteile der einzelnen Zwischenprodukte im Vergleich zur Matrix
an. Deine Aufgabe ist es nun, die Zu- und Abnahme der Anteile der einzelnen Zwischenprodukte im Vergleich zur Matrix  in einer neuen Matrix anzugeben.
Die Zu- und Abnahme der Zwischenprodukte im Bezug zur Matrix
in einer neuen Matrix anzugeben.
Die Zu- und Abnahme der Zwischenprodukte im Bezug zur Matrix  ergibt sich aus der Differenz der beiden Matrizen. Willst du die Differenz der Matrizen
ergibt sich aus der Differenz der beiden Matrizen. Willst du die Differenz der Matrizen  und
und  berechnen und so die Matrix
berechnen und so die Matrix  bestimmen, in der die Differenz der beiden Matrizen dargestellt wird, so subtrahierst du die zugehörigen Einträge miteinander.
Du könntest dabei so vorgehen:
Die hier gesuchte Matrix ist also:
bestimmen, in der die Differenz der beiden Matrizen dargestellt wird, so subtrahierst du die zugehörigen Einträge miteinander.
Du könntest dabei so vorgehen:
Die hier gesuchte Matrix ist also:

d)
Bestimmen des gesuchten Zwischenproduktvektors  Der Aufgabenstellung kannst du entnehmen, dass ein Kunde eine Bestellung von 7 ME
Der Aufgabenstellung kannst du entnehmen, dass ein Kunde eine Bestellung von 7 ME  , 3 ME
, 3 ME  , 4 ME
, 4 ME  und 11 ME
und 11 ME  aufgegeben hat, wobei der zugehörige Produktionsvektor folgender ist:
aufgegeben hat, wobei der zugehörige Produktionsvektor folgender ist:
 Deine Aufgabe ist es nun, die dafür benötigten ME an Zwischenprodukte zu berechnen und dein Ergebnis in Form eines Zwischenproduktvektors
Deine Aufgabe ist es nun, die dafür benötigten ME an Zwischenprodukte zu berechnen und dein Ergebnis in Form eines Zwischenproduktvektors  anzugeben. Wirfst du einen Blick in deine Formelsammlung zu den Verflechtungsmatrizen, so erkennst du, dass sich der Zwischenproduktvektor
anzugeben. Wirfst du einen Blick in deine Formelsammlung zu den Verflechtungsmatrizen, so erkennst du, dass sich der Zwischenproduktvektor  im Allgemeinen über folgende Multiplikation ergibt:
im Allgemeinen über folgende Multiplikation ergibt:
 mit:
mit:
 und
und  , um die Aufgabe hier zu lösen:
Der hier gesuchte Zwischenproduktvektor
, um die Aufgabe hier zu lösen:
Der hier gesuchte Zwischenproduktvektor  ist also:
ist also:  .
.
: Zwischenprodukt-Endprodukt-Matrix
: Produktionsvektor
2.
a)
Das zugehörige Verflechtungsdiagramm bestimmen
In der Aufgabenstellung ist dir eine Rohstoff-Endprodukt-Matrix gegeben. Deine Aufgabe ist es dabei, das zugehörige Verflechtungsdiagramm zu zeichnen. Willst du zur gegebenen Rohstoff-Endprodukt-Matrix ein Verflechtungsdiagramm zeichnen, so gehst du so vor:
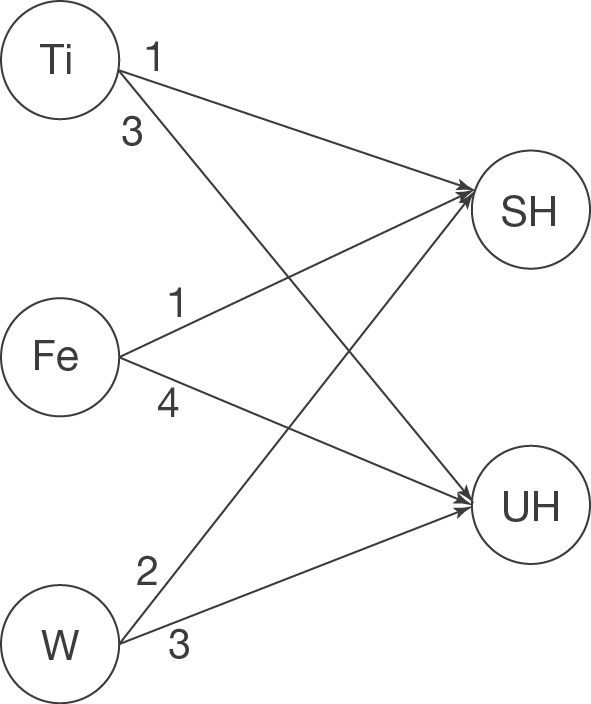
- Zeichne für jeden verwendeten Rohstoff einen Knoten
- Zeichne auf der gegenüberliegenden Seite für jedes Endprodukt einen Knoten
- Verbinde jeden Rohstoffknoten mit den Endproduktknoten über Pfeile
- Schreibe zu jedem Pfeil die verwendeten kg der für die Legierung (Endprodukte) verwendeten Rohstoffe

b)
Formulieren der Matrizengleichung
Formuliere die Matrizengleichung, die den allgemeinen Zusammenhang zwischen dem Produktionsvektor  und dem zugehörigen Rohstoffvektor
und dem zugehörigen Rohstoffvektor  beschreibt. Der allgemeine Zusammenhang zwischen Produktions- und Rohstoffvektor lautet:
beschreibt. Der allgemeine Zusammenhang zwischen Produktions- und Rohstoffvektor lautet:
 mit:
mit:
 ,
,  und
und  in die allgemeine Formel ein, so sieht diese wie folgt aus:
in die allgemeine Formel ein, so sieht diese wie folgt aus:
![\( \begin{array}{rll}
\begin{pmatrix}Ti\\Fe\\W\end{pmatrix}&=&C \cdot \begin{pmatrix}SH\\UH\end{pmatrix}\\[5pt]
\begin{pmatrix}Ti\\Fe\\W\end{pmatrix}&=&\begin{pmatrix}1&3\\1&4\\2&3\end{pmatrix} \cdot \begin{pmatrix}SH\\UH\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/deeaede0a6bccb118738c509ce3d83002af547a17dd097b0e744cb6933f624c3?color=5a5a5a)
: Rohstoffvektor
: Produktionsvektor
: Rohstoff-Endprodukt-Matrix
c)
Den gesuchten Rohstoffvektor  berechnen
Hier sollst du nun berechnen, wie viele Rohstoffe benötigt werden, um 6 kg
berechnen
Hier sollst du nun berechnen, wie viele Rohstoffe benötigt werden, um 6 kg  und 3 kg
und 3 kg  -Legierung herzustellen. Weiterhin musst du dein Ergebnis als Rohstoffvektor
-Legierung herzustellen. Weiterhin musst du dein Ergebnis als Rohstoffvektor  angeben.
Nach dem in Aufgabenteil b gezeigten allgemeinen Zusammenhang zwischen Produktions- und Rohstoffvektor ergibt sich der gesuchte Rohstoffvektor
angeben.
Nach dem in Aufgabenteil b gezeigten allgemeinen Zusammenhang zwischen Produktions- und Rohstoffvektor ergibt sich der gesuchte Rohstoffvektor  , indem du den gegebenen Produktionsvektor mit der Rohstoff-Endproduktmatrix
, indem du den gegebenen Produktionsvektor mit der Rohstoff-Endproduktmatrix  multiplizierst:
Der hier gesuchte Rohstoffvektor ist also:
multiplizierst:
Der hier gesuchte Rohstoffvektor ist also:  .
.
d)
Angeben, wie viel kg  und
und  mit dem Lagerbestand hergestellt werden können
Der Aufgabenstellung kannst du entnehmen, dass im Lager des Schmelzofens 70 kg
mit dem Lagerbestand hergestellt werden können
Der Aufgabenstellung kannst du entnehmen, dass im Lager des Schmelzofens 70 kg  , 90 kg
, 90 kg  und 80 kg
und 80 kg  bereit liegen. Deine Aufgabe ist es dabei, zu berechnen, wie viele kg
bereit liegen. Deine Aufgabe ist es dabei, zu berechnen, wie viele kg  und
und  Legierung mit diesem Lagerbestand hergestellt werden können und dieses Ergebnis als Endproduktvektor
Legierung mit diesem Lagerbestand hergestellt werden können und dieses Ergebnis als Endproduktvektor  anzugeben.
Aus den vorherigen Aufgabenteilen weißt du, dass der allgemeine Zusammenhang zwischen Rohstoff- und Endproduktvektor lautet:
anzugeben.
Aus den vorherigen Aufgabenteilen weißt du, dass der allgemeine Zusammenhang zwischen Rohstoff- und Endproduktvektor lautet:

 sowie
sowie  ein, so ergibt sich hier zunächst folgende Gleichung:
ein, so ergibt sich hier zunächst folgende Gleichung:
![\( \begin{array}{rll}
\vec{r}&=&C \cdot \vec{p}\\[5pt]
\begin{pmatrix}70\\90\\80\end{pmatrix}&=&\begin{pmatrix}1&3\\1&4\\2&3\end{pmatrix}\cdot \begin{pmatrix}SH\\UH\end{pmatrix}\\[5pt]
\begin{pmatrix}70\\90\\80\end{pmatrix}&=&\begin{pmatrix}1 \cdot SH &+& 3\cdot UH\\1 \cdot SH &+& 4\cdot UH\\2 \cdot SH &+& 3\cdot UH\end{pmatrix}\\
\end{array}\)](https://mathjax.schullv.de/fb297658040d293228f04e399ab58e22efe766ad4885b2f97af0bdb2315175b4?color=5a5a5a) Dieses Ergebnis kannst du als Gleichungssystem mit drei Gleichungen und zwei Unbekannten formulieren und mittels Additions- oder Subtraktionsverfahren lösen. Verwende dabei eine der Gleichungen, um dein Ergebnis zu verifizieren.
Es ergibt sich also:
Dieses Ergebnis kannst du als Gleichungssystem mit drei Gleichungen und zwei Unbekannten formulieren und mittels Additions- oder Subtraktionsverfahren lösen. Verwende dabei eine der Gleichungen, um dein Ergebnis zu verifizieren.
Es ergibt sich also:  und
und  . Verwende nun Gleichung Ⅲ um dein Ergebnis zu verifizieren:
. Verwende nun Gleichung Ⅲ um dein Ergebnis zu verifizieren:
 Da sich Gleichung Ⅲ mit
Da sich Gleichung Ⅲ mit  und
und  zu einer wahren Aussage ergibt, lautet hier der gesuchte Produktionsvektor:
zu einer wahren Aussage ergibt, lautet hier der gesuchte Produktionsvektor:

3.
a)
1. Schritt: Rohstoff-Zwischenprodukt-Matrix bestimmen
Beschreibe zunächst den gegebenen Verflechtungsgraphen, der die Verteilung der Rohstoffe auf die Zwischenprodukte angibt, durch eine Rohstoff-Zwischenprodukt-Matrix. Eine Rohstoff-Zwischenprodukt-Matrix setzt sich so zusammen:
 entspricht also einer
entspricht also einer  -Matrix. Beim Erstellen dieser Matrix
-Matrix. Beim Erstellen dieser Matrix  kann es hilfreich sein, wenn du diese und deren Einträge zunächst in einer Tabelle einträgst:
kann es hilfreich sein, wenn du diese und deren Einträge zunächst in einer Tabelle einträgst:
Aus dieser Tabelle ergibt sich die hier gesuchte Matrix  wie folgt:
wie folgt:
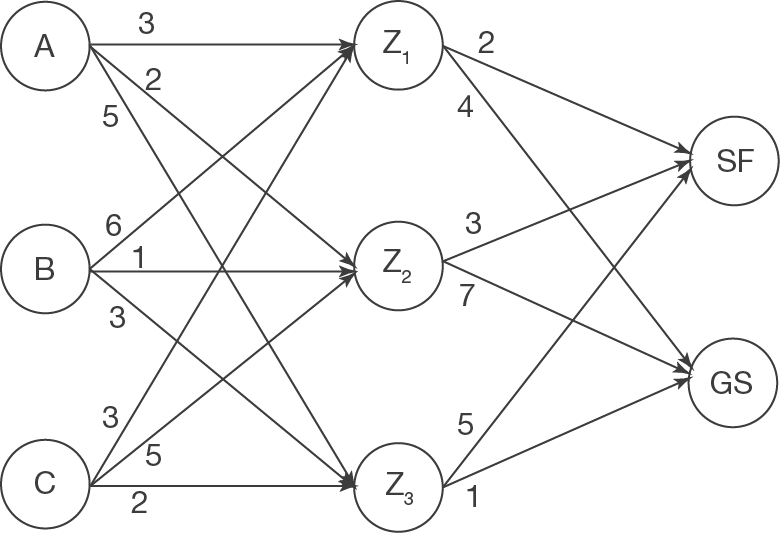
 2. Schritt: vollständigen Verflechtungsgraphen bestimmen
Nun sollst du ausgehend vom bereits gegebenen Teil des Verflechtungsgraphen und der Zwischenprodukt-Endprodukt-Matrix den vollständigen Verflechtungsgraphen erstellen. Gehe dabei so vor:
2. Schritt: vollständigen Verflechtungsgraphen bestimmen
Nun sollst du ausgehend vom bereits gegebenen Teil des Verflechtungsgraphen und der Zwischenprodukt-Endprodukt-Matrix den vollständigen Verflechtungsgraphen erstellen. Gehe dabei so vor:
- Sie besitzt genau so viele Zeilen, wie es Rohstoffe gibt
Hier hat die Matrix insgesamt 3 Zeilen
- Sie besitzt genau so viele Spalten, wie es Zwischenprodukte gibt
Hier hat die Matrix insgesamt 3 Spalten
- Die Matrixeinträge ergeben sich aus den Mengeneinheiten der Rohstoffe, die für eine ME eines Zwischenproduktes nötig sind
| Zwischenprodukte | |||
| Rohstoffe | |||
| 3 | 2 | 5 | |
| 6 | 1 | 3 | |
| 3 | 5 | 2 | |
- Zeichne für jedes Endprodukt einen Knoten
- Verbinde jeden Zwischenproduktknoten mit den Endproduktknoten über Pfeile
- Schreibe zu jedem Pfeil die verwendeten ME, der für die Präparate (Endprodukte) verwendeten Zwischenprodukte

b)
1. Schritt: Matrizengleichung formulieren
Hier sollst du zunächst die Matrizengleichung formulieren, die den allgemeinen Zusammenhang zwischen dem Produktionsvektor  und dem zugehörigen Rohstoffvektor
und dem zugehörigen Rohstoffvektor  beschreibt. Der allgemeine Zusammenhang zwischen Produktions- und Rohstoffvektor lautet:
beschreibt. Der allgemeine Zusammenhang zwischen Produktions- und Rohstoffvektor lautet:
 mit:
mit:
 ,
,  und
und  in die allgemeine Formel ein, so sieht diese wie folgt aus:
in die allgemeine Formel ein, so sieht diese wie folgt aus:
 2. Schritt: Rohstoff-Endprodukt-Matrix bestimmen
Die Rohstoff-Endprodukt-Matrix ergibt sich über das Matrizenprodukt zwischen Rohstoff-Zwischenprodukt-Matrix und Zwischenprodukt-Endprodukt-Matrix, wobei gilt:
2. Schritt: Rohstoff-Endprodukt-Matrix bestimmen
Die Rohstoff-Endprodukt-Matrix ergibt sich über das Matrizenprodukt zwischen Rohstoff-Zwischenprodukt-Matrix und Zwischenprodukt-Endprodukt-Matrix, wobei gilt:
 mit:
mit:
 zu bestimmen:
Die Rohstoff-Endprodukt-Matrix
zu bestimmen:
Die Rohstoff-Endprodukt-Matrix  ist hier also:
ist hier also:

: Rohstoffvektor
: Produktionsvektor
: Rohstoff-Endprodukt-Matrix
: Rohstoff-Zwischenprodukt-Matrix
: Zwischenprodukt-Endprodukt-Matrix
: Rohstoff-Endprodukt-Matrix
c)
1. Schritt: Bestimmen der ME an Rohstoffen
Der Aufgabenstellung kannst du entnehmen, dass ein Großkunde insgesamt 100 ME der Super-Fit und 200 ME der Guter-Schlaf-Präparate bestellt. Deine Aufgabe ist es nun, zu berechnen, wie viele ME an Rohstoffen  ,
,  und
und  dafür benötigt werden.
Es gilt:
dafür benötigt werden.
Es gilt:
 mit:
mit:
 und berechne über ein Matrizenprodukt den zugehörigen Rohstoffvektor
und berechne über ein Matrizenprodukt den zugehörigen Rohstoffvektor  , der dir angibt, wie viele Rohstoffe für das Bedienen der Bestellung benötigt werden.
Mit
, der dir angibt, wie viele Rohstoffe für das Bedienen der Bestellung benötigt werden.
Mit  ergibt sich hier:
Der hier gesuchte Rohstoffvektor ist also:
ergibt sich hier:
Der hier gesuchte Rohstoffvektor ist also:  . Es werden also 9.900 ME an Rohstoff
. Es werden also 9.900 ME an Rohstoff  , 9.800 ME an Rohstoff
, 9.800 ME an Rohstoff  und 12.900 an Rohstoff
und 12.900 an Rohstoff  benötigt.
2. Schritt: Bestimmen der ME an Zwischenprodukten
Nun sollst du noch berechnen, wie viele ME an Zwischenprodukte für den erteilten Auftrag benötigt werden. Es gilt:
benötigt.
2. Schritt: Bestimmen der ME an Zwischenprodukten
Nun sollst du noch berechnen, wie viele ME an Zwischenprodukte für den erteilten Auftrag benötigt werden. Es gilt:
 mit
mit
 mit dem Produktionsvektor
mit dem Produktionsvektor  , um hier die ME der benötigten Zwischenprodukte zu bestimmen:
Der hier gesuchte Zwischenproduktvektor ist also:
, um hier die ME der benötigten Zwischenprodukte zu bestimmen:
Der hier gesuchte Zwischenproduktvektor ist also:  .
Es werden also 1.000 ME an Zwischenprodukt
.
Es werden also 1.000 ME an Zwischenprodukt  , 1.700 ME an Zwischenprodukt
, 1.700 ME an Zwischenprodukt  und 700 an Zwischenprodukt
und 700 an Zwischenprodukt  benötigt.
benötigt.
: Rohstoffvektor
: Produktionsvektor
: Rohstoff-Endprodukt-Matrix
: Zwischenproduktvektor
: Produktionsvektor
: Zwischenprodukt-Endprodukt-Matrix
d)
Berechnen, wie viele ME der einzelnen Rohstoffe noch benötigt werden
Der Aufgabenstellung kannst du entnehmen, dass ein anderer Kunde 100 ME von  und 150 ME von
und 150 ME von  bestellt. Um diesen Auftrag zu bedienen, werden aus dem Zwischenlager 200 ME von
bestellt. Um diesen Auftrag zu bedienen, werden aus dem Zwischenlager 200 ME von  und 100 ME von
und 100 ME von  verwendet.
verwendet.
Berechne, wie viele ME der einzelnen Rohstoffe für diesen Auftrag noch benötigt werden. Um zu bestimmen, wie viele ME an Rohstoffen noch benötigt werden, musst du zunächst berechnen, wie viele ME an Zwischenprodukten überhaupt noch hergestellt werden müssen, um den Auftrag zu bedienen. Hast du dies bestimmt, so berechnest du über den passenden Zusammenhang, wie viele ME an Rohstoffen verwendet werden müssen, um die Zwischenprodukte herzustellen. Gehe hier so vor: in den oben genannten Zusammenhang für den Zwischenproduktvektor
in den oben genannten Zusammenhang für den Zwischenproduktvektor  einsetzt und wie folgt berechnest:
2. Schritt: ME der zu produzierenden Zwischenprodukte bestimmen
Aus der Aufgabenstellung weißt du, dass 200 ME von
einsetzt und wie folgt berechnest:
2. Schritt: ME der zu produzierenden Zwischenprodukte bestimmen
Aus der Aufgabenstellung weißt du, dass 200 ME von  und 100 ME von
und 100 ME von  aus dem Lager für den Auftrag verwendet werden. Schreibe dies nun als Zwischenproduktvektor
aus dem Lager für den Auftrag verwendet werden. Schreibe dies nun als Zwischenproduktvektor  , um diesen dann vom eben berechneten Zwischenproduktvektor
, um diesen dann vom eben berechneten Zwischenproduktvektor  zu subtrahieren. So berechnest du nämlich, wie viele Zwischenprodukte (Vektor
zu subtrahieren. So berechnest du nämlich, wie viele Zwischenprodukte (Vektor  ) für den Auftrag neu gefertigt werden müssen.
3. Schritt: ME der zu benötigten Rohstoffe bestimmen
Die Mengeneinheiten der benötigten Rohstoffe berechnest du, indem du den eben bestimmten Zwischenproduktvektor
) für den Auftrag neu gefertigt werden müssen.
3. Schritt: ME der zu benötigten Rohstoffe bestimmen
Die Mengeneinheiten der benötigten Rohstoffe berechnest du, indem du den eben bestimmten Zwischenproduktvektor  in den oben genannten Zusammenhang für den Rohstoffvektor
in den oben genannten Zusammenhang für den Rohstoffvektor  einsetzt und wie folgt berechnest:
Für den Auftrag werden also 7.550 ME an Rohstoff
einsetzt und wie folgt berechnest:
Für den Auftrag werden also 7.550 ME an Rohstoff  , 6.800 ME an Rohstoff
, 6.800 ME an Rohstoff  und 9.350 ME an Rohstoff
und 9.350 ME an Rohstoff  benötigt.
benötigt.
Berechne, wie viele ME der einzelnen Rohstoffe für diesen Auftrag noch benötigt werden. Um zu bestimmen, wie viele ME an Rohstoffen noch benötigt werden, musst du zunächst berechnen, wie viele ME an Zwischenprodukten überhaupt noch hergestellt werden müssen, um den Auftrag zu bedienen. Hast du dies bestimmt, so berechnest du über den passenden Zusammenhang, wie viele ME an Rohstoffen verwendet werden müssen, um die Zwischenprodukte herzustellen. Gehe hier so vor:
- Bestimme die ME der benötigten Zwischenprodukte:
- Bestimme die ME der zu produzierenden Zwischenprodukte: Verwende die Angabe das 200 ME von
und 100 ME von
aus dem Lager verwendet werden
- Bestimme die ME der benötigten Rohstoffe: