Übergangsgraphen
Wenn du einen Übergangsgraphen zeichnen sollst, hast du entweder einen Text, indem alle wichtigen Informationen gegeben sind, oder eine Übergangsmatrix gegeben.
Egal was dir vorliegt, du kannst immer gleich vorgehen.
der Kunden von A dem Hersteller treu, 
der Kunden wechseln zum Hersteller M und 
wechseln zum Hersteller S.
Dagegen bleiben 
dem Hersteller S treu, wechseln zu M und wechseln zum Hersteller A.
Dem Hersteller M bleiben 
treu, 
wechseln zum Hersteller A und wechseln zum Hersteller S.
Bilde den zugehörigen Übergangsgraphen.
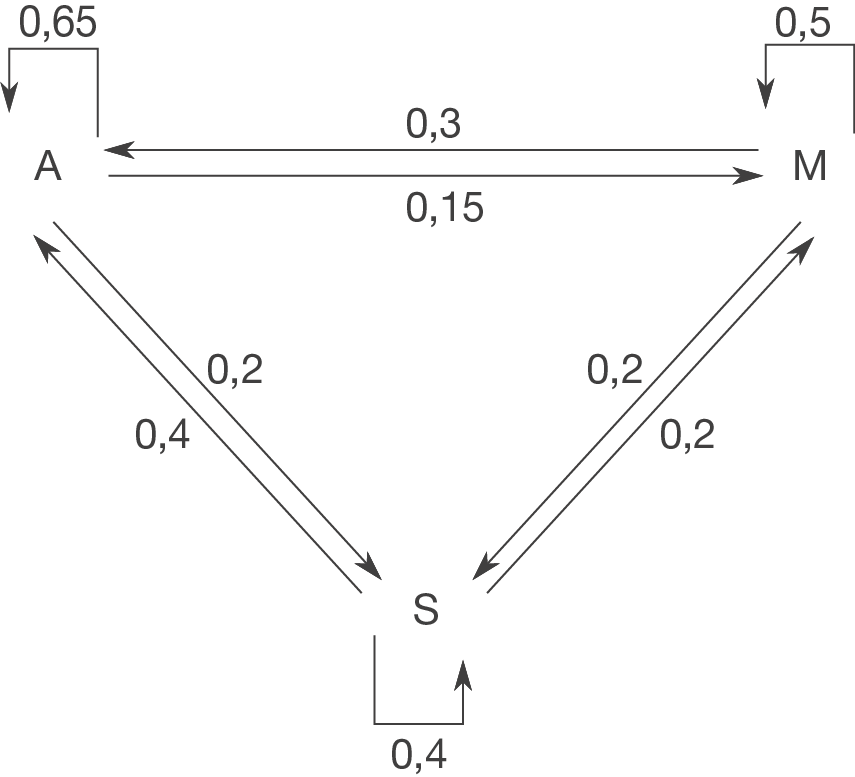
- Schreibe als erstes die Zustände die gegeben sind auf, also zum Beispiel die verschiedenen Unternehmen, die involviert sind, oder die verschiedenen Stadien einer Art.
- Verbinde die Zustände mit passenden Pfeilen und beschrifte diese mit den dazugehörigen Anteilen bzw. Übergangs-wahrscheinlichkeiten. Ein Pfeil mit der Beschriftung
von
nach
bedeutet z.B., dass in jedem Zeitschritt
der Kunden von
Beispiel
Der Markt von Tablet-PCs wird im wesentlichen von drei Herstellern A, S und M beherrscht. Nach einem Jahr bleiben
1.
Stelle die durch die Matrix 
beschriebenen Übergänge in einem Übergangsgraphen (Über- gangsdiagramm) dar.
a)
| von: | ||||||
| nach: | ||||||
b)
| von: | ||||||
| nach: | ||||||
c)
| von: | ||||||
| nach: | ||||||
d)
| von: | ||||||
| nach: | ||||||
e)
| von: | ||||||
| nach: | ||||||
f)
| von: | ||||||
| nach: | ||||||
2.
Stelle die im Text beschriebenen Übergänge in einem Übergangsgraphen (Übergangsdiagramm) dar.
a)
Ein Restaurant bietet Plätze in drei Bereichen an: der Gäststätte, im Biergarten und auf der Dachterrasse. Über das Verhalten der Stammkunden des Restaurants sei bekannt:
der Stammkunden wählen bei ihrem nächsten Besuch wieder den gleichen Bereich.
- Von den Stammkunden, die in der Gaststätte aßen, wechseln bei ihrem nächsten Besuch
auf die Dachterrasse und
in den Biergarten.
- Von den Stammkunden, die im Biergarten aßen, wechseln bei ihrem nächsten Besuch
- Von den Stammkunden, die auf der Dachterrasse aßen, wechseln bei ihrem nächsten Besuch
in die Gaststätte und
b)
Ein Reisebüro bietet Reisen per Bahn, per Schiff und per Flug an. Über die letzten Jahre hinweg konnte das Reisebüro folgende Erfahrungswerte ermitteln:
- Von den Reisenden, die per Flug gereist sind, wählen
auch bei ihrer nächsten Reise das Flugzeug.
- Von den Reisenden, die per Bahn gereist sind, wählen
- Von den Reisenden, die per Schiff gereist sind, wählen
wieder das Schiff. Die anderen
steigen bei ihrer nächsten Reise auf das Flugzeug um.
c)
Ein Fortbildungsangebot besteht aus drei unterschiedlichen Seminaren, die die Teilnehmer nacheinander besuchen und auch bestehen müssen. Wenn ein Teilnehmer ein Seminar nicht besteht, so darf es einmal wiederholen; besteht er es ein zweites Mal nicht, so muss er die Fortbildung abbrechen.
Darüber hinaus gibt es auch Teilnehmer, die die Fortbildung aus Zeitgründen oder anderen persönlichen Motiven abbrechen bzw. auf einen späteren Zeitpunkt verschieben.
Über die letzten Jahre ließen sich folgende Erfahrungswerte ermitteln:
- Von den Teilnehmern an Seminar 1 nehmen im Anschluss
müssen Seminar 1 wiederholen. Die anderen scheiden aus dem Programm aus.
- Von den Teilnehmern an Seminar 2 nehmen im Anschluss
an Seminar 3 Teil;
müssen Seminar 2 wiederholen. Die restlichen scheiden aus dem Programm aus.
- Von den Teilnehmern an Seminar 3 schließlich bestehen
.
müssen Seminar 3 wiederholen, die restlichen
d)
Eine Kontaktbörse im Internet bietet kostenpflichtige Mitgliedschaften für 3 Monate, 6 Monate und 12 Monate an. Nach Ablauf der Mitgliedschaft können die Nutzer sich für eine weitere Mitgliedschaft auf 3, 6 oder 12 Monate entscheiden, oder das Angebot verlassen.
Im Rahmen einer Werbekampagne bietet die Kontaktbörse für die bestehenden Nutzer die Möglichkeit an, neue Nutzer für eine Mitgliedschaft auf 3, 6, oder 12 Monate zu werben.
Die Unternehmensleitung geht von folgendem Kundenverhalten aus:
- Von den Nutzern, die eine Mitgliedschaft auf 3 Monate gebucht haben, entscheiden sich im Anschluss
- Von den Nutzern, die eine Mitgliedschaft auf 6 Monate gebucht haben, entscheiden sich im Anschluss
- Von den Nutzern, die eine Mitgliedschaft auf 12 Monate gebucht haben, entscheiden sich im Anschluss
3.
In der Kantine einer Firma werden täglich drei Gerichte angeboten: Essen 1 (E1), Essen 2 (E2), sowie ein vegetarisches Menü (V).
Einige Stammkunden wählen am nächsten Mittag jeweils das gleiche Gericht, andere entscheiden sich für ein anderes. Das Wahlverhalten der Stammkunden der Kantine ist in folgendem Übergangsgraphen (Übergangsdiagramm) dargestellt:
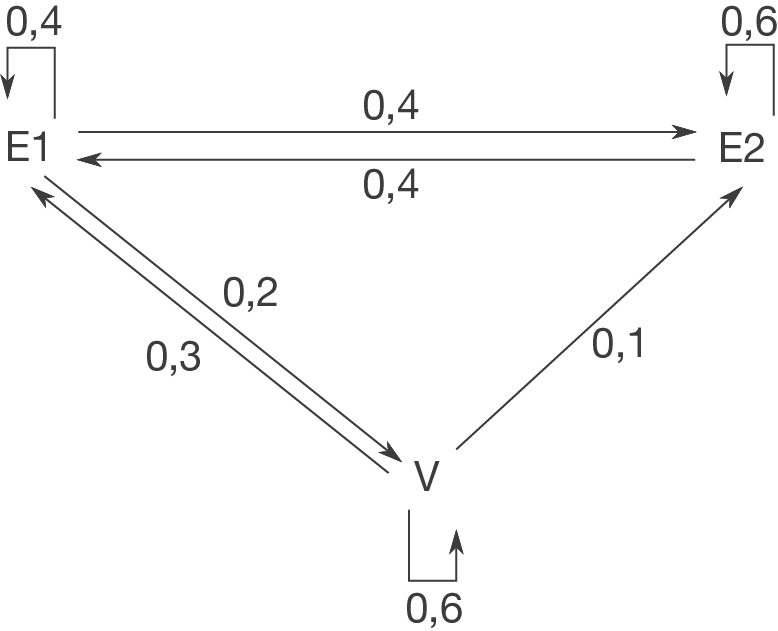Beschreibe das Verhalten der Stammkunden der Kantine in Worten.
4.
Die Bücher eines Autors werden als Bücher mit Hardcover (B), Taschenbuch (T) und als Hörbücher (H) verkauft. Eine Umfrage ergab, dass die Leser sich beim nächsten Buch des Autors oft für den gleichen Buchtyp enscheiden, dass aber auch ein Wechselverhalten vorliegt.
Dieses Leserverhalten ist in folgendem Übergangsgraphen (Übergangsdiagramm) dargestellt:
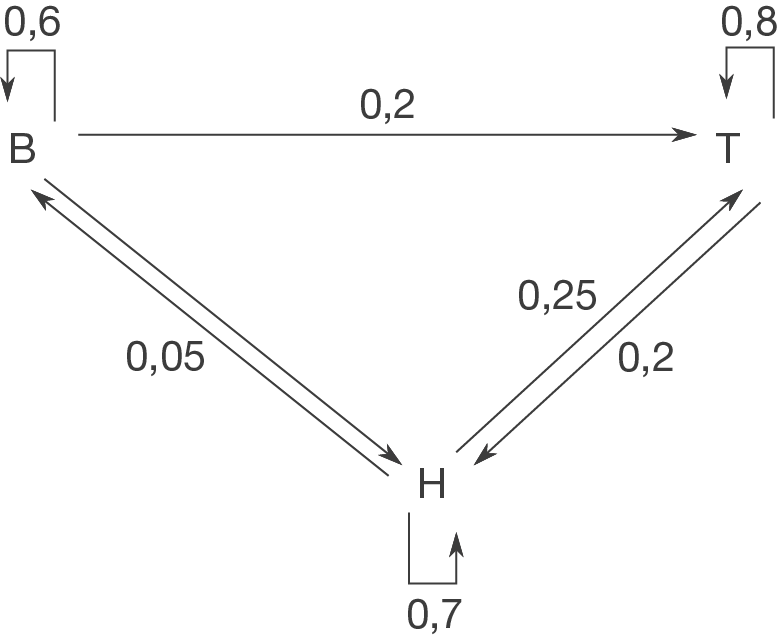Beschreibe das Verhalten der Leser in Worten.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
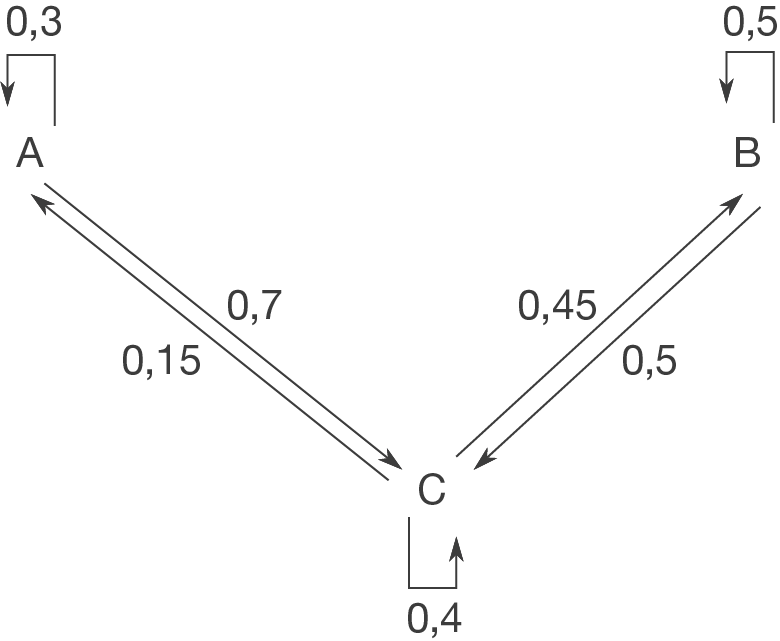
b)
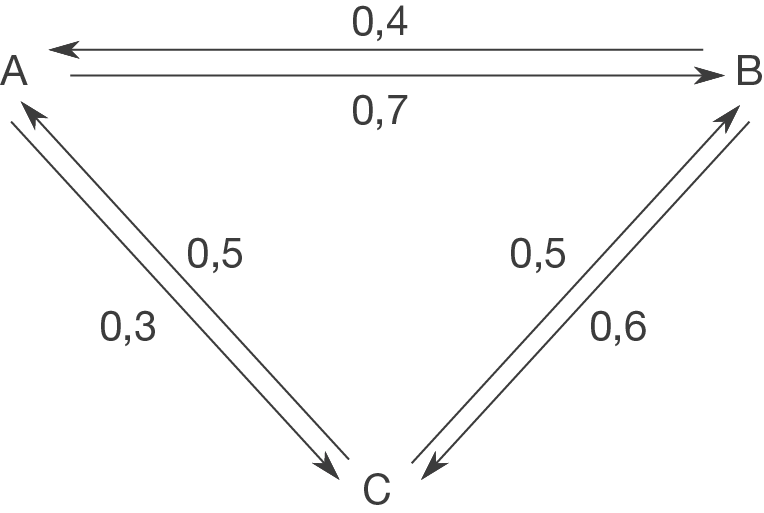
c)
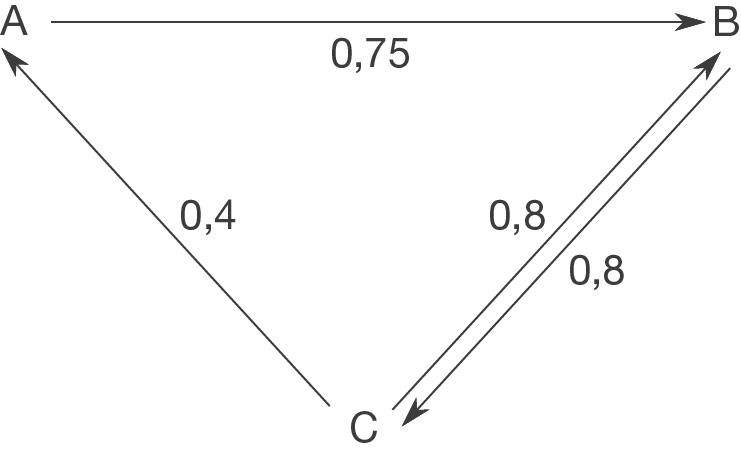
d)
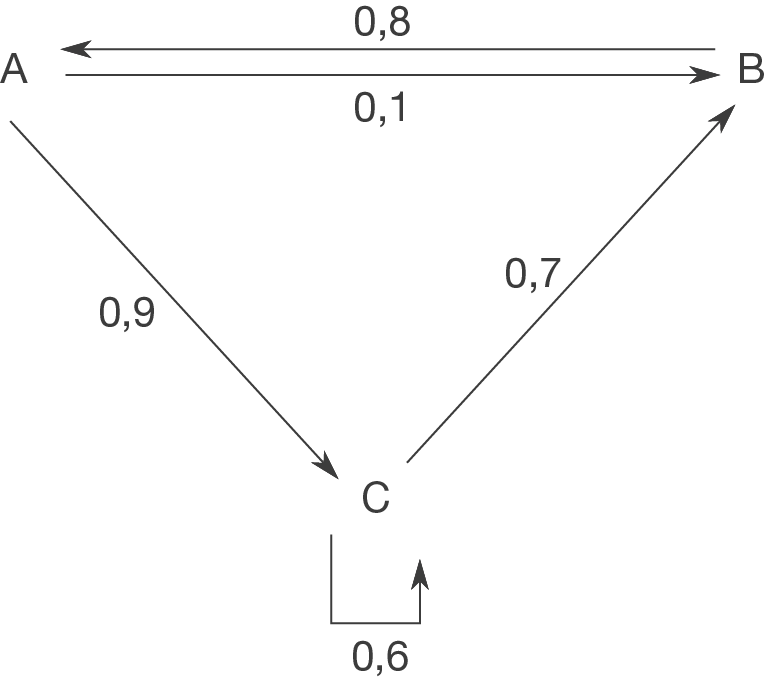
e)
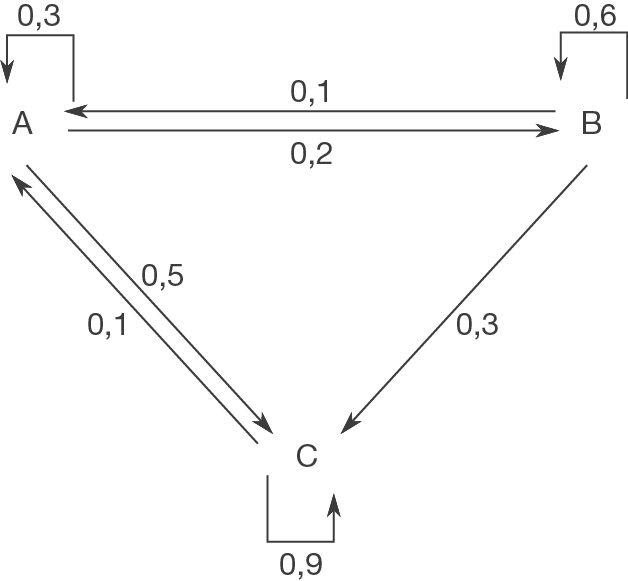
f)
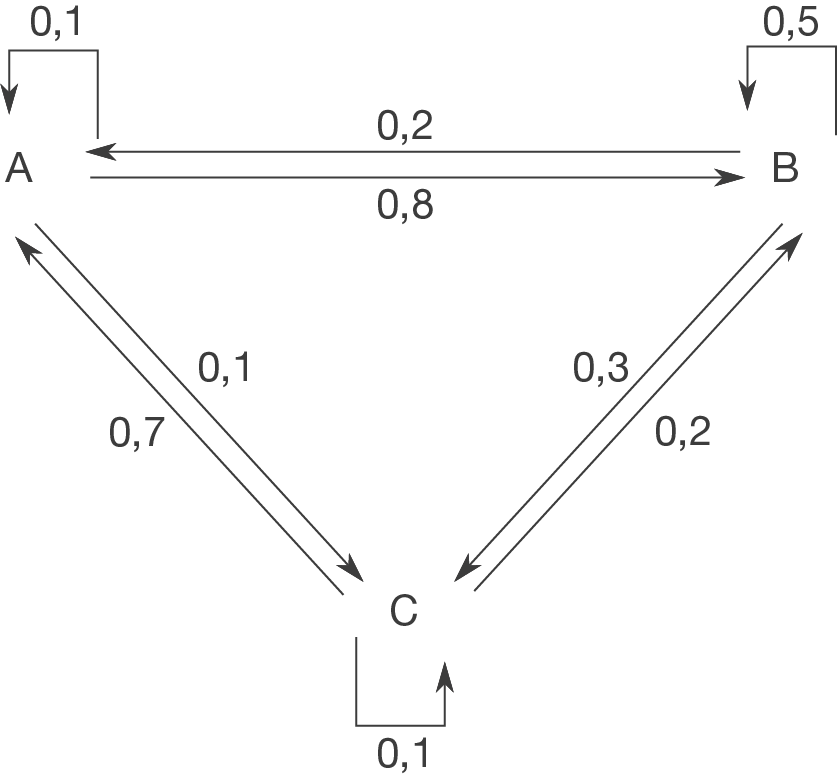
2.
a)
Wir kürzen die Gaststätte mit G, den Biergarten mit B und die Dachterrasse mit D ab. Dann ergibt sich aus dem Text folgendes Diagramm:
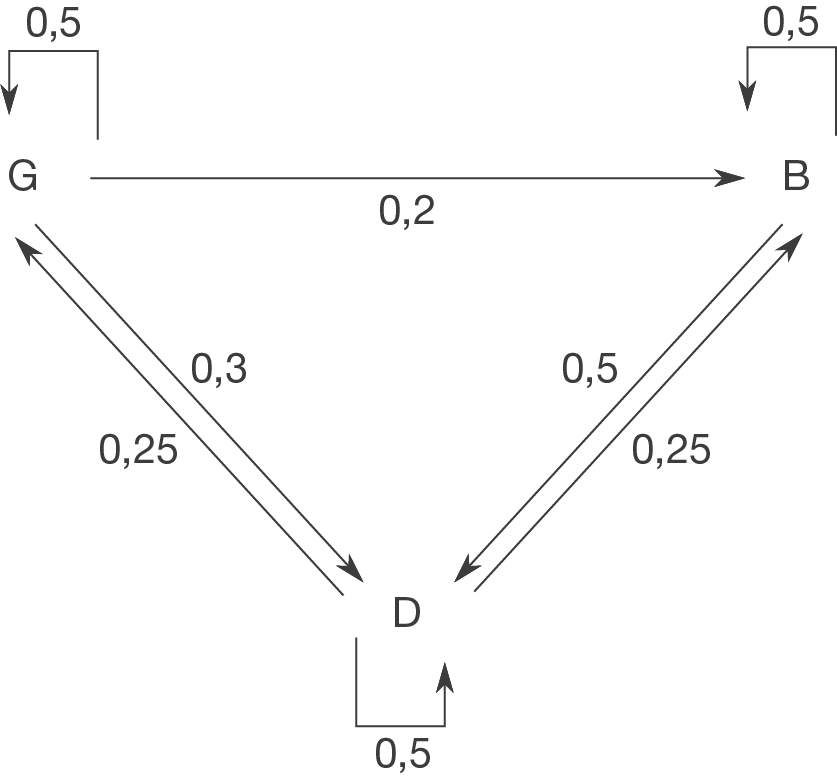
b)
Wir kürzen die Bahn mit B, das Schiff mit S und den Flug mit F ab. Dann ergibt sich aus dem Text folgendes Diagramm:
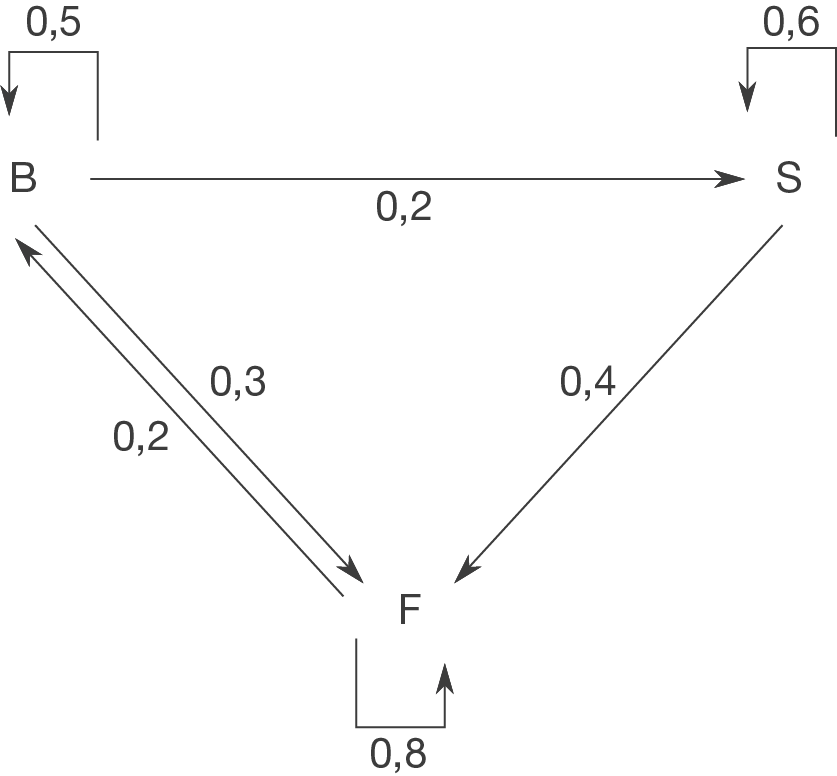
c)
Wir kürzen die drei Seminare mit S1, S2 und S3 ab. Dann ergibt sich aus dem Text folgendes Diagramm:
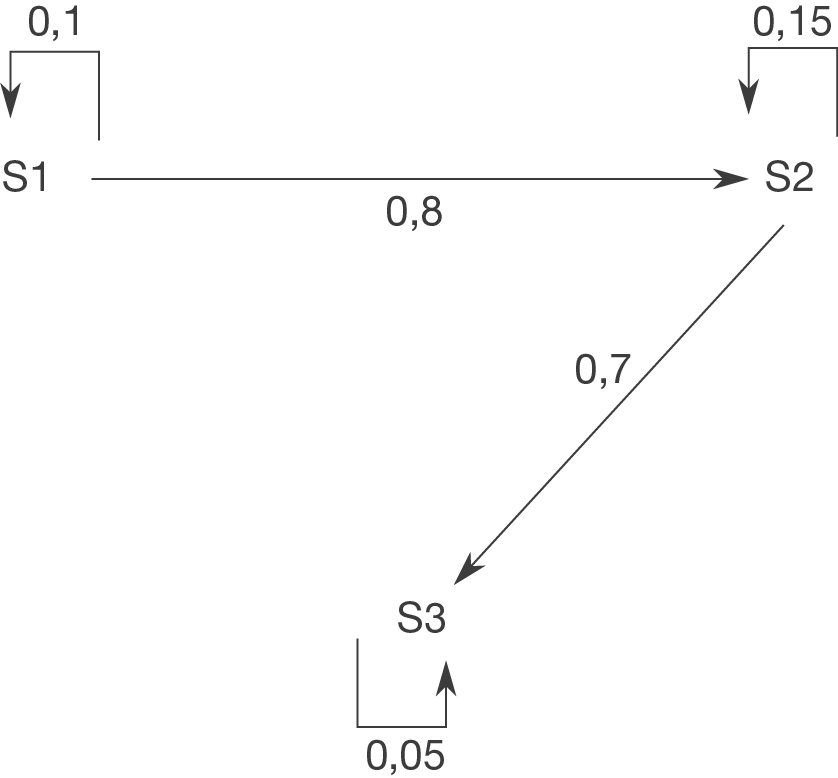
d)
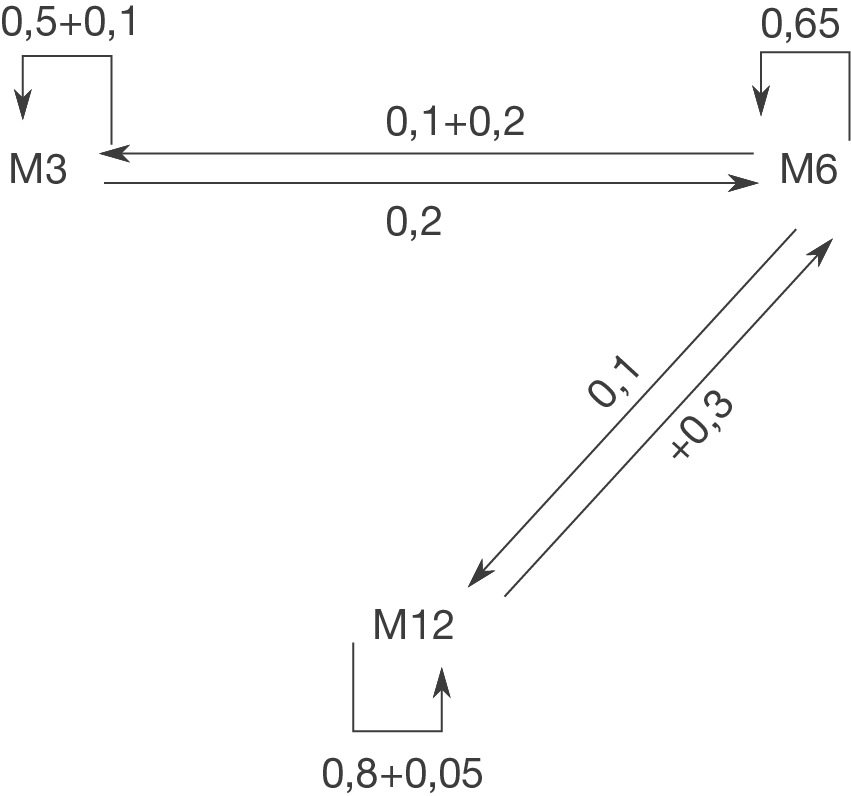
Wir kürzen die drei Laufzeiten mit M3, M6 und M12 ab. Anders als bei den vorherigen Aufgaben scheint es hier zwei Arten von Übergängen zu geben. Beachte allerdings: die Übergänge beziehen sich nur auf die Anzahl der Personen, nicht auf die Personen selbst.
Wenn also der Nutzer, die eine M3 gebucht hatten, wieder M3 buchen, so ergibt sich an dieser Stelle im Übergangsgraphen zunächst der Wert 0,5.
Nun ist aber bekannt, dass dieser Nutzer einen weiteren Nutzer für M3 anwerben. Der relative Anteil der neuen an den alten Nutzern entspricht nun als 
.
Mit dieser Überlegung ergibt sich der Übergangsgraph:
3.
Betrachte die drei Zustände einzeln und beschreibe die jeweiligen Übergänge:
- Von den Stammkunden, die Essen 1 bestellt haben, wählen am nächsten Mittag
- Von den Stammkunden, die sich für Essen 2 entschieden haben, wählen am nächsten Mittag
- Von den Stammkunden, die sich für das vegetarische Menü entschieden haben, wählen am nächsten Mittag
4.
Betrachte die drei Zustände einzeln und beschreibe die jeweiligen Übergänge:
- Von den Lesern, die sich das Buch mit Hardcover gekauft haben, entscheiden sich
beim nächsten Buch wieder für ein Buch mit Hardcover,
wählen das Taschenbuch und
- Von den Lesern, die sich das Taschenbuch gekauft haben, entscheiden sich
wieder für das Taschenbuch und
- Von den Lesern, die sich das Hörbuch gekauft haben, entscheiden sich
wieder für das Hörbuch,
für das Taschenbuch und
kaufen das Buch mit Hardcover.